二叉搜索树

树的条件

1. 树节点增加key属性，用来比较谁大谁小，key不可以重复
2. 左节点保存小数值，相反右节点保存大数值

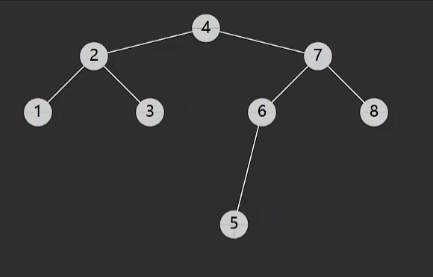
注意

二叉搜索树极端情况会退化成链表

树退化成链表情况

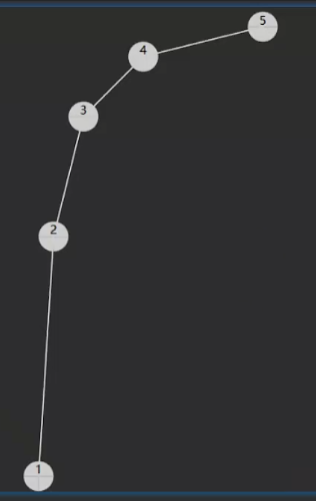
节点

class TreeNode<V> {
    int key;
    V value;
    TreeNode left;
    TreeNode right;

    public TreeNode() {
    }

    public TreeNode(int key, V value) {
        this.key = key;
        this.value = value;
    }

    public TreeNode(int key, V value, TreeNode left) {
        this.key = key;
        this.value = value;
        this.left = left;
    }

    public TreeNode(int key, V value, TreeNode left, TreeNode right) {
        this.key = key;
        this.value = value;
        this.left = left;
        this.right = right;
    }
}

get

get根据树的定义，在遍历的时候只需要判断当前节点大于还是小于，如果是大于那么查找右边，相反就查找左边

递归实现

public V get(int key) {
    if (root == null) {
        return null;
    }
    return doGet(root, key);
}

private V doGet(TreeNode node, int k) {
    if (node.key > k) {
        return doGet(node.left, k);
    } else if (node.key < k) {
        return doGet(node.right, k);
    } else {
        return (V) node.value;
    }
}

遍历实现

public V get(int key) {
    if (root == null) {
        return null;
    }
    TreeNode<V> p = root;
    while (p != null) {
        //当前节点大于，向左边查找
        if (p.key > key) {
            p = p.left;
        } else if (p.key < key) {
            //当前节点小于，向右边查找
            p = p.right;
        } else {
            return p.value;
        }
    }
    return null;
}

put

put需要注意的是，插入前先寻找传入的key，如果存在那么就更新，不存在就判断插入的key，跟上一个比较，如果大就右边，小左边

public void put(int k, V v) {
    //根节点为null，当前设置为根节点
    if (root == null) {
        root = new TreeNode(k, v);
        return;
    }
    TreeNode p = root;
    //需要插入节点的上一个节点
    TreeNode preParent = null;
    while (p != null) {
        preParent = p;
        if (p.key > k) {
            //当前节点大于k，向左寻找
            //如：p.key = 4，传入的key是3 
            p = p.left;
        } else if (p.key < k) {
            //向右寻找
            p = p.right;
        } else {
            //当前key存在，进行更新
            p.value = v;
            break;
        }
    }

    TreeNode node = new TreeNode(k, v);
    if (k > preParent.key) {
        preParent.right = node;
    } else {
        preParent.left = node;
    }
}

前任节点

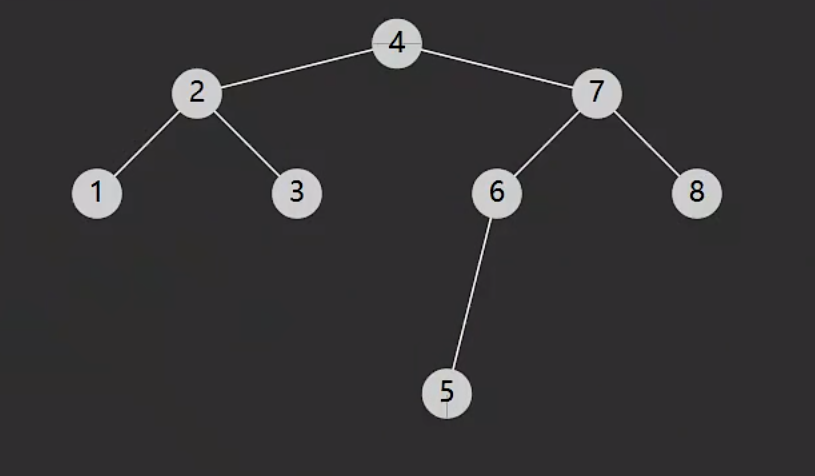
定义：

• 节点有左子树，此时前任就是左子树的最大值
• 节点没有左子树，若离它最近的、自左而来的祖先就是前任

举例

1. 5的前仍就是4
2. 3 前任是2
3. 1 没有前任

/**
 *  前继着
 */
public V successor(long k) {
    if (root == null) {
        return null;
    }
    TreeNode p = root;
    TreeNode ancestorFromLeft = null;
    while (p != null) {
        if (p.key > k) {
            p = p.left;
        } else if (p.key < k) {
            //自左而来以上图为例
            //p.right 说明key存在左边，但是left 说明节点是放在右边
            //比如4，4就是存放在左边的节点，6也是从右而来所以也不是
            ancestorFromLeft = p;
            p = p.right;
        } else {
            break;
        }
    }

    //没找到节点
    if (p == null) {
        return null;
    }
    //1.节点有左子树，此时前任就是左子树的最大值
    //2.节点没有左子树，若离它最近的、自左而来的祖先就是前任
    if (p.left != null) {
        //情况一
        return max(p.left);
    } else {
        //情况二
        return ancestorFromLeft == null ? null : (V) ancestorFromLeft.value;
    }
}

后任节点

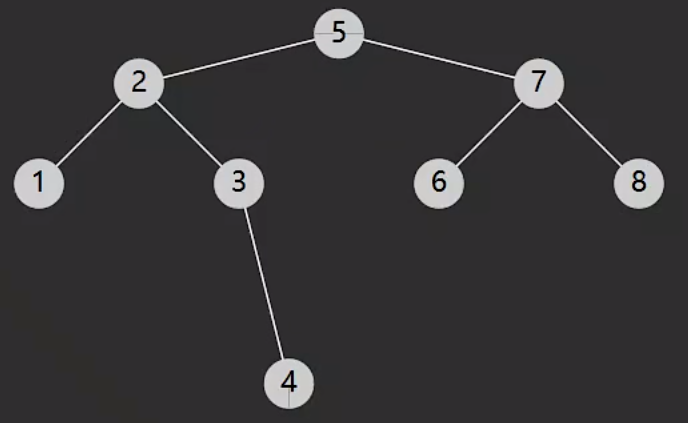
定义

• 节点有右子树，此时后继节点即为右子树的最小值
• 节点没有右子树，若离它最近的祖先自从右而来，此祖先即为后继

举例

1. 2的后任是3
2. 4 的后任是null
3. 5的后任是6

/**
 * 后继者
 */
public V predecessor(long k) {
    if (root == null) {
        return null;
    }
    TreeNode p = root;
    TreeNode ancestorFromRight = null;
    while (p != null) {
        if (p.key > k) {
            p = p.left;
            ancestorFromRight = p;
        } else if (p.key < k) {
            p = p.right;
        } else {
            break;
        }
    }

    //没找到节点
    if (p == null) {
        return null;
    }
    //1.节点有右子树，此时后继节点即为右子树的最小值
    //2.节点没有左子树，若离它最近的、自左而来的祖先就是前任
    if (p.right != null) {
        //情况一
        return doMin(p.right);
    } else {
        //情况二
        return ancestorFromRight == null ? null : (V) ancestorFromRight.value;
    }
}

delete

关键代码说明

1. 找节点最小值：在删除节点之前先要找到节点，找到节点之后获取当前节点左子节点最小值，（按照下图就是找到了5节点）

while (s.left != null) {
    sParent = s;
    s = s.left;
}

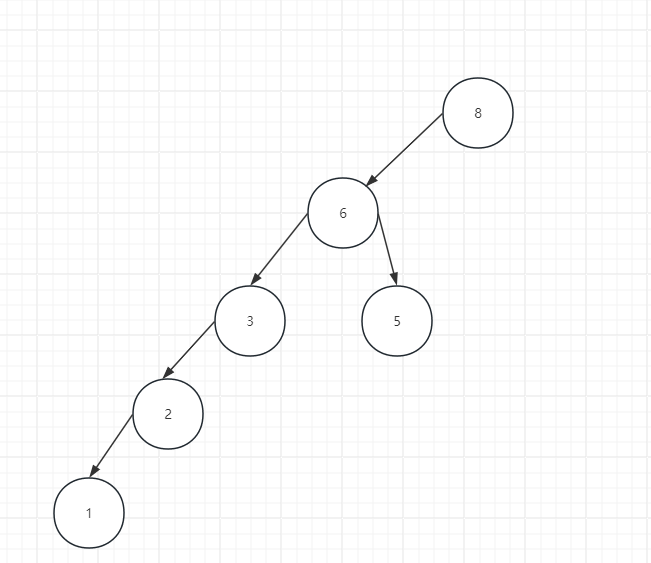
2. 两种情况
   1. 以上图举例（如果是相邻，那么sparent 就是5，p也是5）
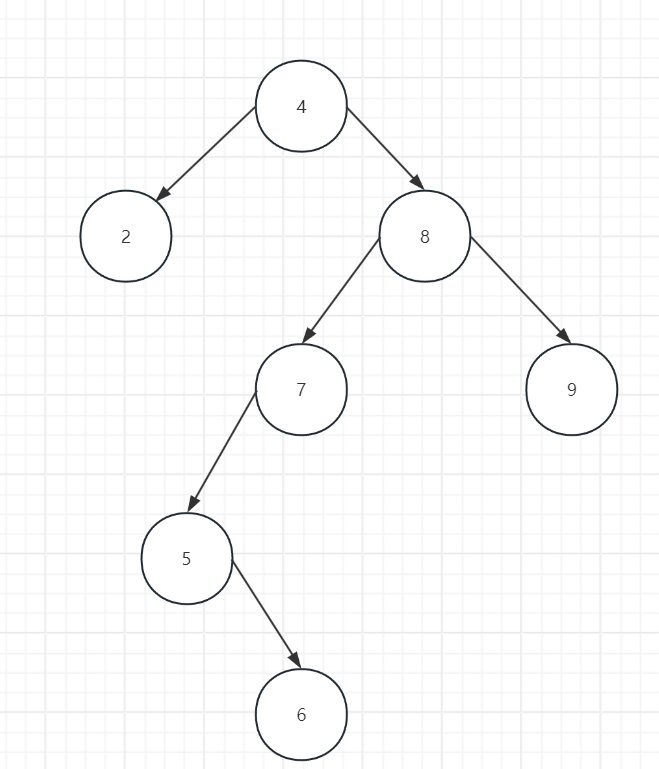
   2. 后节点不是5了。看下图 ，如果删除4那么后节点应该是5，但是通过1情况寻找之后，他们就不会相邻了。所以会进入条件
      1. 此时 sParent = 7，p = 4

if (sParent != p) {
    //处理后继的后事
    shift(sParent, s, s.right);
    //替换之后将右节点替换成原先的右节点
    s.right = p.right;
}

public V delete(int k) {
    if (root == null) {
        return null;
    }
    TreeNode p = root;
    TreeNode preParent = null;
    while (p != null) {
        if (p.key > k) {
            preParent = p;
            p = p.left;
        } else if (p.key < k) {
            preParent = p;
            p = p.right;
        } else {
            break;
        }
    }

    if (p == null) {
        return null;
    }

    //删除节点没有左孩于，将右孩子托孤给Parent
    if (p.left == null) {
        shift(preParent, p, p.right);
    }
    //删除节点没有右孩子，将左孩子托孤给Parent
    else if (p.right == null) {
        shift(preParent, p, p.left);
    } 
    //删除节点左右孩子都有，可以将它的后继节点（称为S)托孤给Parent
    else {
        //被到节点的后继，最小值
        TreeNode s = p.right;
        TreeNode sParent = null;
        
        while (s.left != null) {
            sParent = s;
            s = s.left;
        }
        
        //判断是不是原先的相邻父节点
        if (sParent != p) {
            //处理后继的后事
            shift(sParent, s, s.right);
            //替换之后将右节点替换成原先的右节点
            s.right = p.right;
        }
        //后继取代被刷除节点
        shift(preParent, p, s);
        s.left = p.left;
    }
    return (V) p.value;
}

/**
 * @param root   被删除节点的父亲
 * @param remove 被删除节点
 * @param child  被顶上去的节点
 */
private void shift(TreeNode root, TreeNode remove, TreeNode child) {
    if (root == null) {
        //为空把顶层的树节点赋值为child
        this.root = child;
    } 
    //判断节点放在左边还是右边
    else if (root.left == remove) {
        root.left = child;
    } else {
        root.right = child;
    }
}