# AVL 树

如果在插入和删除时通过旋转，始终让二叉搜索树保持平衡，称为自平衡的二叉搜索树
AVL树是在二叉搜索树上的优化，二叉搜索树理想状态是左子树存储数值小的节点，相反右节点存储大的

但是在极端情况下二叉搜索树会退化成链表

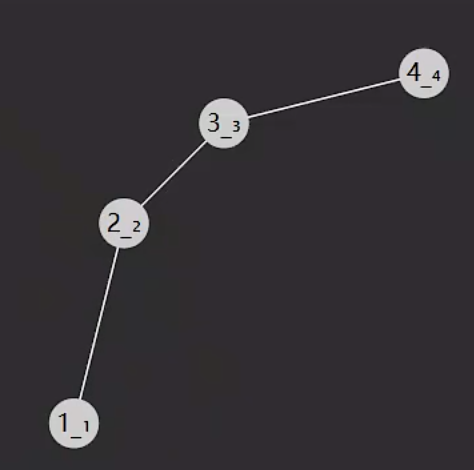
img.树的退化

这种情况就需要右旋/左旋

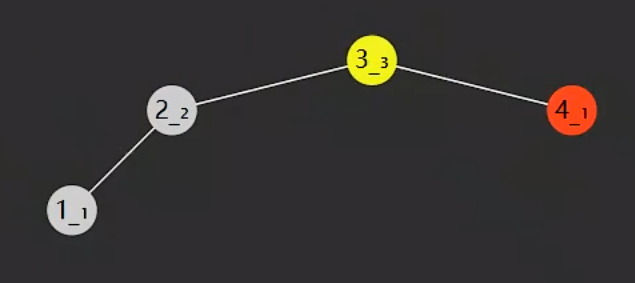
旋转条件

如果一个节点的左右孩子，高度差超过1，则此节点失衡，才需要旋转

# 旋转情况

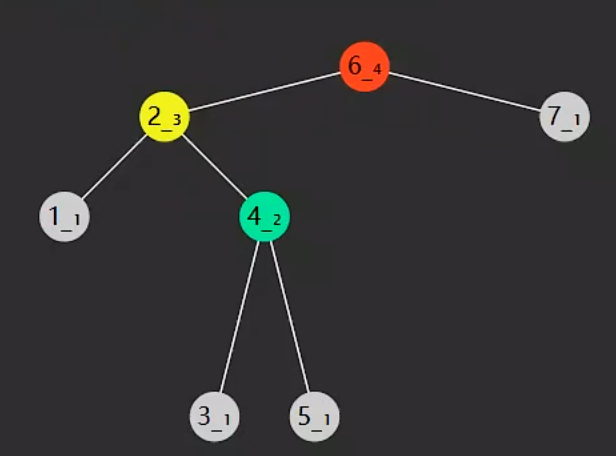
理想状态下通过右旋/左旋可以解决不平衡问题，但是也会有其他其情况左子树节点高，向右旋转

右旋
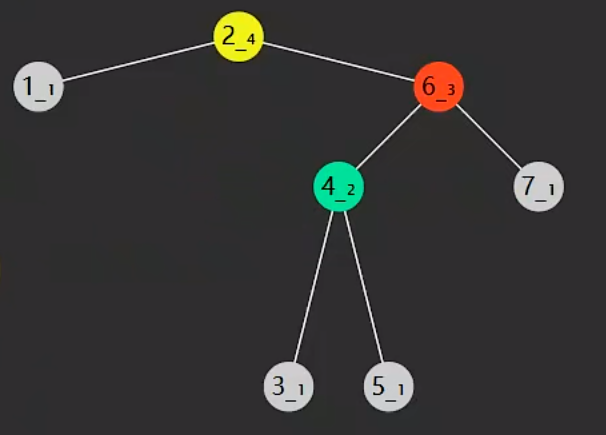
右旋之后树的高度还是不平衡

# 四种失去平衡情况

# 左左

失衡节点,左边更高
失衡节点左孩子，即左孩子这边也是左边更高或等与

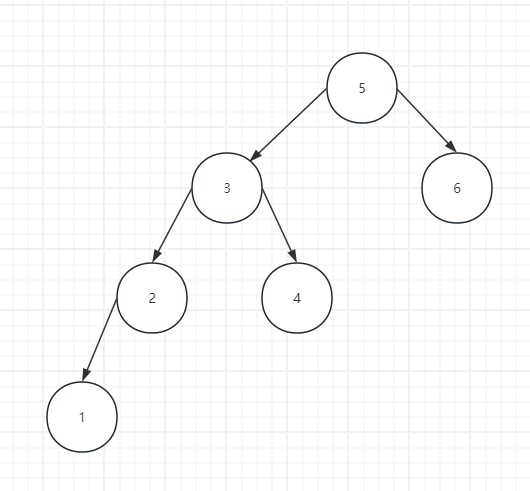
# 左右

失衡节点,即左边更高
失衡节点的左孩子,即左孩子这边是右边更高

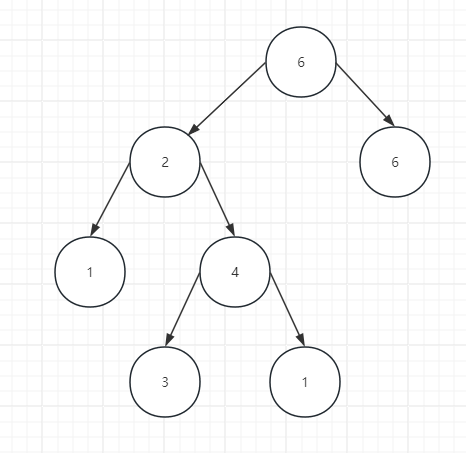
# 右左

失衡节点,即右边更高
失衡节点的右孩子，即右孩子这边左边更高

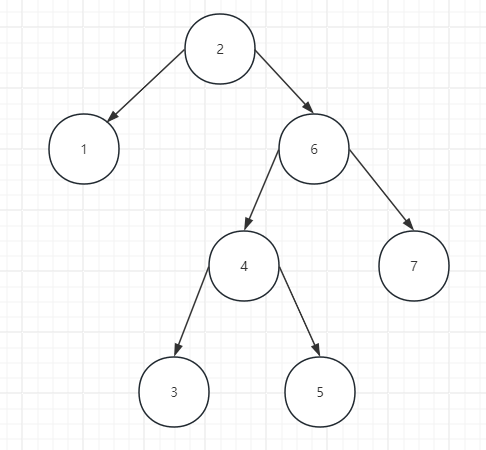
# 右右

失衡节点,即右边更高
失衡节点的右孩子,即右孩子这边右边更高或等高

# 核心方法

# 树的高度和修改高度

    /**
     * 获取节点高度
     */
    private int height(AVLNode avlNode) {
        return avlNode == null ? null : avlNode.height;
    }

    /**
     * 修改节点高度
     */
    private void updateHeight(AVLNode avlNode) {
        avlNode.height = Integer.max(height(avlNode.left), height(avlNode.right)) + 1;
    }

# 左旋

/**
 * 左旋
 */
private AVLNode leftRotate(AVLNode avlNode) {
    AVLNode right = avlNode.right;
    AVLNode oldLeft = right.right;
    right.right = avlNode;
    avlNode.left = oldLeft;
    return right;
}

# 右旋

/**
 * 右旋
 */
private AVLNode rightRotate(AVLNode avlNode) {
    //left作为新根节点返回
    AVLNode left = avlNode.left;
    //暂存原先的左节点的右子树
    AVLNode oldRight = left.right;
    //进行右旋，left作为根节点，原先的更节点转移到右侧
    left.right = avlNode;
    //进行右旋之后，原先的avlNode变成了右子树，并且将原先的avlNode左节点的右节点，转移到avlNode的左节点
    avlNode.left = oldRight;
    updateHeight(avlNode);
    updateHeight(left);
    return left;
}

# 左旋+右旋

也就是 LL / RL

private AVLNode leftRightRotate(AVLNode avlNode) {
    avlNode.left = leftRotate(avlNode.left);
    return rightRotate(avlNode);
}

private AVLNode RightLeftRotate(AVLNode avlNode) {
    avlNode.right = rightRotate(avlNode.right);
    return leftRotate(avlNode);
}

# 平衡

平衡判断条件

/**
 * 平衡因子  = 左子树高度 - 右子树高度
 * @return
 *  0，-1，1 在平衡条件中
 *  大于1：左子树高
 *  小于-1 右子树高
 */
private int balanceFactor(AVLNode avlNode) {
    return height(avlNode.left) - height(avlNode.right);
}

private AVLNode balance(AVLNode avlNode) {
    if (avlNode == null) {
        return null;
    }
    int bf = balanceFactor(avlNode);
    if (bf > 1 && (balanceFactor(avlNode.left) >= 0)) {
        //LL
        return rightRotate(avlNode.left);
    } else if (bf > 1 && (balanceFactor(avlNode.left) < 0)) {
        //LR
        return leftRightRotate(avlNode.left);
    } else if (bf < -1 && (balanceFactor(avlNode.right) > 0)) {
        //RL
        return RightLeftRotate(avlNode.right);
    } else if (bf < -1 && (balanceFactor(avlNode.right) <= 0)) {
        //RR
        return leftRotate(avlNode.right);
    }
    return avlNode;
}

# put

    public void put(int key, Object value) {
        root = doPut(root, key, value);
    }

    private AVLNode doPut(AVLNode node, int key, Object value) {
        //1. 找到空位，进行插入
        if (node == null) {
            return new AVLNode(key, value);
        }
        //2. key存在，进行更新
        if(node.key == key){
            node.value = value;
            return node;
        }
        //3. 继续查找
        if (node.key < key) {
            //向左查找
            node.left = doPut(node.left, key, value);
        } else {
            //向右
            node.right = doPut(node.right, key, value);
        }
        //更新高度
        updateHeight(node);
        //检查是否平衡
        return balance(node);
    }

# 删除

 private AVLNode delete(int key) {
        return root = doDelete(key, root);
    }

    private AVLNode doDelete(int key, AVLNode node) {
        //1. 节点不存在
        if (node == null) {
            return null;
        }
        //2. 没找到key
        if (node.key < key) {
            node = doDelete(key, node.right);
        } else if (node.key > key) {
            node = doDelete(key, node.left);
        } else {
            //3. 找到key
                //3.1 节点没有子节点
            if (node.left == null && node.right == null) {
                node = null;
            } else if (node.right == null) {
                //3.2 节点只有左节点
                node = node.left;
            } else if (node.left == null) {
                //3.3 节点只有右节点
                node = node.right;
            } else {
                //3.4 节点左右节点都有
                AVLNode s = node.right;
                //寻找后继节点
                while (s.left != null) {
                    s = s.left;
                }
                s.right = doDelete(s.key, node.right);
                s.left = node.left;
                node = s;
            }
        }
        //4.更新高度
        updateHeight(node);
        //5.平衡
        return balance(node);
    }

← 二叉搜索树链表 →